|

|
1)
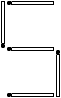
LOS CUADRADOS: Mueve cuatro fósforos y forma
tres cuadrados.
|
 |
|
2)
Con la misma cantidad de fósforos utilizada en
el número cinco se puede escribir su doble.
¿Cómo lo harías?
|
 |
|
3)¿Podrías
transformar 16 fósforos en “nueve” sin quitar
ninguno? ¿Cómo lo harías?
|
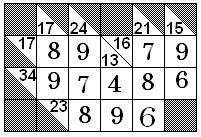
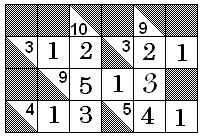
 |
| |
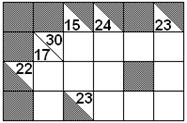
|
|
4)
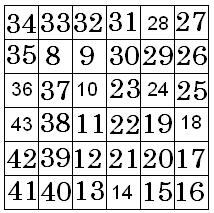
En
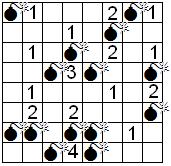
un número de dos cifras, la decena es igual al doble de
la unidad.
La
diferencia entre ambas cifras es tres. ¿Cuál es el
número?
|
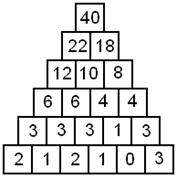
5)
PIRÁMIDE NUMÉRICA: Encuentra los números que
faltan en la
pirámide, de manera que el número que está
ubicado en una casilla
sea la suma de los números de las dos casillas
sobre las que se apoya.
|
 |
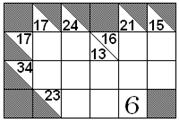
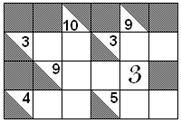
6)
Completar los espacios en blanco de modo tal que en cada
casillero, excepto en el primero y en el segundo, el
número que se coloque sea igual a la suma de los dos
anteriores.
7)
Escribir todos los números capicúas de tres cifras en
los cuáles aparece el siete. ¿Cuántas veces aparece el
siete en estos números que escribiste?
|
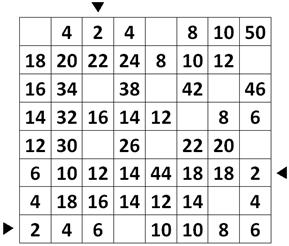
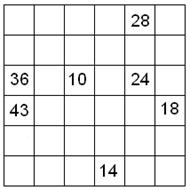
8)
LABERINTO NUMÉRICO: Entre por una de las
casillas que tienen el número 2 y pase de una
casilla a otra vecina en forma horizontal o
vertical, siempre sumando dos, hasta llegar al
50. Las casillas en blanco son comodines; allí
podrás anotar los números que necesites para
seguir avanzando, pero usando sólo una vez cada
comodín.
|
 |
9)
Sabiendo que un elefante y un ratón, juntos, pesan una
tonelada y 100 gramos, y que el peso del elefante es
igual al peso del ratón más una tonelada, ¿Cuánto pesa
cada uno de los animales?
10)
Marta, Micaela y Ana van al cine a ver una película. La
madre, además del dinero para la entrada, ha dado a las
tres hermanas una cantidad de dinero a repartir
equitativamente entre las tres y que cada una podrá
gastar como prefiera.
Marta, la hermana mayor, entrega la parte
correspondiente a cada una de sus hermanas, pero Ana se
da cuenta de que Micaela tiene el doble de dinero que
ella y, a su vez, Micaela descubre que Marta tiene el
doble que el suyo.
Si
Ana tiene 6 monedas, ¿cuántas debería tener cada de las
tres hermanas si la división se hubiese realizado de
manera correcta?
11)
Manuel tiene 54 años y tres hijos. Las edades de sus
hijos son divisores de su edad. Sabemos que la edad del
mayor es un número compuesto par; la edad del segundo es
un número compuesto par que es el doble de la edad del
hijo menor. ¿Qué edad tiene cada hijo?
|
12)
SUDOKU CON LETRAS: Completar los casilleros
vacíos con las letras A, B, C, D, E y F, de modo
que no se repita ninguna de ellas en ninguna
fila, columna ni en cada cuadrícula.
|
 |
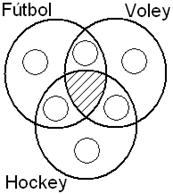
13)
En el Club Deportivo Victoria acaban de cerrar la
inscripción para entrenar en distintos deportes. El
diagrama les permite analizar el número de inscriptos en
las distintas actividades para socios de 12 y 13 años,
teniendo en cuenta que hay socios que participarán en
más de una.
Se
pide volcar correctamente en el diagrama la información
dada.
a)
El total de inscriptos es 78.
b)
35 se anotaron en voley.
c)
20 sólo jugarán hockey y 26 sólo voley.
d)
Ninguna persona se anotó para entrenar en los
tres deportes.
e)
4 entrenarán sólo voley y fútbol.
f)
63 se anotaron para practicar sólo un deporte.
|
En
esta misma categoría (12 – 13 años) se
inscribieron 30 socios para practicar natación o
tenis, y la mitad de ellos son niñas.
Si
10 niñas practican tenis y 11 natación, ¿Cuántas
practican los dos deportes?
|
 |
14)
DIÁLOGO NUMÉRICO: Leyendo atentamente el siguiente texto
puede observarse que en algunas palabras se esconden
números.
a)
¿Podrías indicarlos a medida que los encuentres?
b)
¿Cuántos números hay en total?
b)
¿Cuál es la suma de todos los números del texto?
-¡Hola, Bruno! Necesito que renueves la póliza de
seguro. Recién me llamaron de la agencia, como todos los
fines de mes, para recordármelo.
-Voy papá. Al regresar, ¿puedo comprar pochoclos?
-Sí, pero con la condición de que los comas después del
almuerzo. Mirá que mamá preparó milanesas con puré y
postres exquisitos. Y apuráte que está tormentoso.
-Entonces salgo ya, antes que se largue el aguacero.
-¡Ah! Hijo. Si hacés a tiempo pasá por la panadería de
don Ponce y traé una docena de facturas, pues esta tarde
vienen tía Emilce y el tío Milton a tomar unos mates.
15)
El cuadrado de la figura está dividido en cuatro
cuadriláteros más pequeños mediante dos segmentos
paralelos a sus lados. En tres de ellos se ha escrito el
perímetro correspondiente, ¿Podrías obtener el perímetro
de cada una de las zonas sombreadas?
ACLARACIÓN: El cuadrilátero de perímetro 1 metro es un
cuadrado.

16)
Un fabricante de juguetes quiere sacar al mercado una
nueva línea de reproducciones de automóviles. Desea
hacerlos de madera, metal o plástico, pero no combinar
estos materiales.
No
ha decidido si hacerlos antiguos o modernos, grandes o
pequeños. Teniendo en cuenta estas posibles
combinaciones, ¿de cuántas formas diferentes podría
hacerlos?
17)
Cada una de las siguientes figuras constituye un
rompecabezas con cuyas piezas puede armarse un cuadrado.
Recorta cada figura y divídela en tantas piezas como
indiquen sus divisiones internas. Si logras combinar
adecuadamente las piezas de cualquiera de ellas,
obtendrás un cuadrado.
 
18)
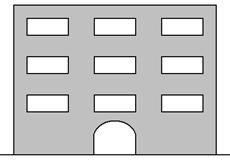
NUEVE VECINOS: Con los datos brindados a continuación se
pide averiguar en que departamento vive cada vecino.
a) María es vecina de Horacio.
b) Laura, Horacio y Diana viven en pisos diferentes.
c) Pablo, Carolina y Diana viven en el mismo piso.
d) Alfredo vive justo arriba de Beatriz, y Beatriz justo
arriba de Diana.
e) Mirando de frente el edificio, Pablo vive en un
departamento ubicado a la izquierda del de Diana, pero
no junto a éste.
f) El departamento de Romina está ubicado entre otros
dos, y justo sobre el de Horacio.
g) Sólo hay un varón por piso.
19)
SUMAS CRUZADAS: Anote en cada casilla una cifra del 1 al
9, de modo que las sumas en horizontal y vertical sean
las que aparecen en las casillas negras. Encima de la
diagonal para las horizontales y debajo de la diagonal
para las verticales. Dentro de un mismo número ninguna
cifra se repite.
20)
Partiendo de la casilla indicada por la flecha, debes
salir por abajo recorriendo TODAS las letras del panal,
sin pasar dos veces por una misma letra y armar de esa
manera una frase. Escríbela.

21)
En una Terminal parte un tren del ramal “A” cada hora;
uno del ramal “B”, cada hora y media; y uno del ramal
“C” cada 48 minutos. A las 8 horas salió un tren de cada
ramal, ¿a qué hora volverán a coincidir los tres trenes
en el horario de partida?
|
22)
Reemplaza cada letra por un número de una cifra,
de modo que cumplan con la operación dada (cada
letra tiene un valor único)
|
 |
|
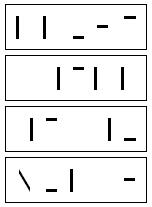
23)
¿Qué palabra se forma al superponer estos
rectángulos?
|
 |
|
24)
EL SABUESO: Un sabueso recorrió todo un campo
cuadriculado, con avances horizontales y
verticales. Arrancó de una casilla con un
número, y fue numerándolas desde allí
sucesivamente. Reconstruya el recorrido. |
 |
|
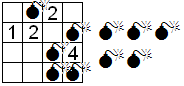
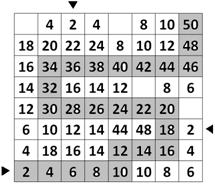
25)
BOMBAS: Detecte las bombas en estos campos
minados. Cada número indica cuántas bombas hay
en las casillas vecinas, en horizontal, vertical
y diagonal. Ninguna casilla lleva más de una
bomba, y donde hay número no hay bomba. Junto a
cada campo se da el total exacto de bombas que
contiene. |
Ejemplo:
 |

S O L U C I O N E S
|
1) |
 |
|
2) |
 |
|
3) |
 |
|
4) |
63 |
|
5) |
 |
|
6) |
 |
|
7) |
171 272 373 474 575 676 777 878 979 707 717
727 737 747 757 767 787 797. Aparece 29
veces |
|
8) |
 |
|
9) |
Ratón: 50 gramos;
Elefante: 1 tonelada + 50 gramos. |
|
10) |
Cada una debería tener 14 monedas. |
|
11) |
18, 6 y 3 años. |
|
12) |
 |
|
13) |
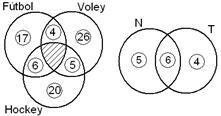 |
|
14) |
b) Hay 14 números; c) 3158 |
|
15) |
a) 3m b) 2,5 m c) 3,5 m d) 4 m e) 4 m |
|
16) |
De 12 formas diferentes. |
|
17) |
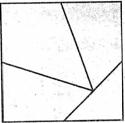 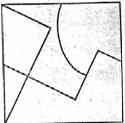
|
|
18) |
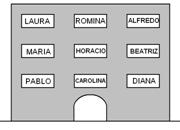 |
|
19) |

|
|
20) |
LA REALIDAD NO ES MAS QUE UNA REGIÓN DENTRO
DE LA FANTASÍA |
|
21) |
A las 20 horas. |
|
22) |
Hay varias, esta es una :

|
|
23) |

|
|
24) |
 |
|
25) |
|
|
 Matan Matan
     
|
|
|
Olimpíada de Matemática y Juegos de Ingenio
del Partido de La Matanza |
|
|
E N T R E N A M I E N T O
2.010
Nivel 2 |
|
|
1)
Doce fósforos conforman cuatro cuadrados,
como se muestra en la figura. Quite dos
fósforos sin mover los restantes, de tal
forma que queden dos cuadrados (no
necesariamente congruentes). |
 |
| |
|
|
2)
Una persona conduce su automóvil y se da cuenta de que
el número que
marca el
cuentakilómetros, 15.951, es un número palíndromo (es
decir,
que se
puede leer tanto desde la derecha como desde la
izquierda).
“¡Qué
extraño! -se dice-.¡Quién sabe cuánto tiempo tendrá que
pasar
antes de
que esto suceda otra vez!”.
Sin
embargo, sólo dos horas después el cuentakilómetros
marca otro
número
palíndromo.
a)
¿Cuál es ese número?
b)
¿A qué velocidad ha viajado el automovilista
durante estas dos horas?
3)
Disponemos de jaulas y pájaros. Al ubicar cada pájaro en
una jaula, sobra uno. Al ubicar dos pájaros en cada
jaula, sobra una.
¿Cuántos
pájaros y cuántas jaulas tenemos?
4)
Usando calculadora.
a) A la biblioteca de la escuela llegaron
279 libros de matemática para repartir en partes iguales
entre 62 alumnos. Se quiere saber cuántos libros sobran.
¿Cómo se puede resolver usando calculadora?
b) En una calculadora se tecleó 54
x
100, pero se cometió un error ya que se quería
multiplicar por 50. ¿Cómo podemos corregirlo sin borrar
lo que está escrito?
c) Realiza la multiplicación 21
x
55 sin utilizar la tecla del 5.
d) Realiza la división 3422
 8
sin usar la tecla del 8. 8
sin usar la tecla del 8.
|
5)
La suma de las cifras de las dos páginas de la
agenda es igual a diez.
¿Cuál es el número mínimo de páginas que debemos
retroceder para tener de nuevo un total de diez
en ambas páginas? ¿Cuáles son las fechas? |
 |
6)
Analía gastó en Musimundo $ 129 para comprarse, entre
libros de $ 15 cada uno y CD’s de $ 18 cada uno, en
total, ocho artículos. ¿Cuántos libros y cuántos CD’s
compró?
|
7)
LAS BANDERAS: Éstas son las banderas de cinco
países diferentes. Cada color ha sido codificado
con una cifra y cada cifra representa el mismo
color. Las cinco banderas pertenecen a cinco de
estos países: Bélgica, Costa de Marfil, Guinea,
Irlanda, Italia y Mali.
Éstos son los colores de las banderas de seis
países:
Bélgica (negro, amarillo, rojo)
Costa de Marfil
(naranja, blanco, verde)
Guinea (rojo, amarillo, verde)
Irlanda (verde, blanco, naranja)
Italia (verde, blanco, rojo)
Mali (verde, amarillo, rojo) |
 |
¿Cuál es
el país que no está representado?
8)
Dos cometas se observan en forma periódica desde nuestro
planeta. Uno de ellos fue visto por última vez en 2001 y
vuelve cada cinco años. El otro fue visto por última vez
en 2005 y vuelve cada ocho años.
¿Podría indicar cuál será el próximo año en el que
podrán verse simultáneamente?
|
9)
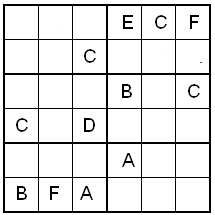
SUDOKU CON LETRAS: Completar los casilleros
vacíos con las letras A, B, C, D, E y F, de modo
que no se repita ninguna de ellas en ninguna
fila, columna ni en cada cuadrícula. |
 |
10)
Descubre el número teniendo en cuenta la información
brindada.
a) Es un
número de seis cifras. La suma de las cifras es 33. La
cifra de las decenas es mayor en una unidad que la cifra
de las unidades. La cifra de las centenas es mayor en
una unidad que la cifra de las decenas, y así
sucesivamente.
b) Al
sumarle dos decenas se convierte en capicúa. Es una
potencia de cuatro. Al dividirlo por 100.000 el
resultado es menor que uno y su primera cifra decimal no
es cero.
c) Es
múltiplo de 20. Es menor que 450 y mayor que 400. Al
dividirlo por 6 el resto es cero.
d) Suma 35
decenas al doble de este número y obtendrás su triplo.
e) Si al
número que buscás le sumás 280, triplicás este resultado
y, luego, sumás 45 a este último producto, obtenés 90
centenas.
f) Si al
doble del número que buscás lo dividís por 5 y duplicás
este resultado, obtenés una decena de mil.
11)
Uno de los niños del equipo de fútbol del barrio realizó
una encuesta entre sus compañeros. La pregunta
respondida fue: “¿Qué color te gustaría para las
camisetas del equipo?”
|
Investiga:
¿Cuántos niños querían camiseta:
a)
de un solo color?
b)
sólo verde?
c)
rojo y amarillo solamente?
d)
de tres colores?
e)
sólo de dos colores?
f)
¿Cuántos niños forman el grupo si todos pudieron
votar? |
 |
|
12)
TAPICES MATEMÁTICOS: Objetivo: Lograr el mayor
puntaje final que sea posible.
Ingresa con cero puntos por cualquiera
de las entradas en la parte superior del tapiz y
trata de acumular el mayor puntaje posible,
realizando las operaciones que se indican en
cada uno de los cuadros blancos, hasta alcanzar
algunas de las salidas en la parte inferior.
Aclaración: El recorrido puede bajar e
ir hacia los costados. |
1) 
2)  |
|
13)
DIBUJOS ENTRECRUZADOS:
a) ¿Qué número está solamente en la
bota y en el bastón?
b) ¿Qué número está solamente en el
sombrero y el bastón?
c) ¿Cuál está solamente en la bota y el
sombrero?
d) ¿Cuánto suman los números que
aparecen solamente en la bota?
|
 |
14)
Los números en las pantallas de las calculadoras,
relojes digitales, etc., se forman usando pequeños
palotes horizontales y verticales.
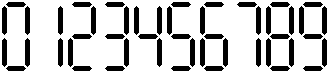
Atento a
esto te contamos lo siguiente. Mariana, Patricia y
Giselle son azafatas. En realidad, una de ellas es
policía y está trabajando de incógnito para investigar
una serie de robos ocurridos durante los vuelos. ¿Querés
saber quién es? Resolvé los calculos, escribí los
resultados en forma ordenada y consecutiva en la
cuadrícula y, observando atentamente, tendrás la
respuesta.

15)
Malena comió, durante los recreos de la mañana, la
quinta parte de la cantidad de galletas que había
llevado, y por la tarde consumió otros dos quintos.
Sabemos que comió 9 galletas en total. ¿Cuántas galletas
llevó al colegio ese día?
16)
En un rectángulo, el largo es el doble del ancho. Si su
perímetro es de 76,50 cm, ¿cuánto mide su largo y su
ancho?
17)
El cuadrado de la figura está dividido en cuatro
cuadriláteros más pequeños mediante dos segmentos
paralelos a sus lados. En tres de ellos se ha escrito el
perímetro correspondiente. ¿Podrías obtener el perímetro
y el área de cada una de las zonas sombreadas?

|
18)
La
figura está formada por un cuadrado y un
triángulo equilátero. ¿Cuánto mide el ángulo
a? |

|
19)
TANGRAM DE LLOYD:

Utilizando
las cinco piezas del tangram de Lloyd y sin
superponerlas, armar las siguientes figuras:
|
a)
Un cuadrado |
b)
Un paralelogramo |
|
 |
 |
20)
¿Qué dígitos se han omitido en la siguiente
multiplicación?
|
|
2 |
* |
* |
|
|
|
* |
* |
|
|
* |
6 |
1 |
|
* |
* |
4 |
|
|
* |
* |
0 |
1 |
21)
KAKURO
Completar
la cuadrícula con un número en cada casilla del 1 al 9,
sin repetir ninguno en la misma fila o columna, de
manera que el total de la suma en cada fila y columna
resulte la cifra indicada.

|
22)
Todos los ases y 10, todas las J, K y Q de un
mazo de barajas francesas se han distribuido
sobre la mesa como indica el gráfico. Para que
puedas descubrir dónde ubicar cada naipe, te
damos algunas pistas: al final de cada columna o
fila se te informa que tipo de cartas la
componen.
Como ayuda, algunos naipes ya han sido
ubicados.
|
 |
|
23)
¿Qué palabra se forma al superponer estos
rectángulos?
|
 |
|
24)
Completa las pirámides dividiendo los dos
ladrillos vecinos; el de la izquierda es el
dividendo y el de la derecha, el divisor. El
cociente se ubica en el ladrillo inferior.
Trabaja con escritura fraccionaria. |
 |
|
25)
Intercala el o los paréntesis necesarios para
que el resultado sea el indicado.
|
 |
|
26)
BOMBAS: Detecte las bombas en estos campos
minados. Cada número indica cuántas bombas hay
en las casillas vecinas, en horizontal, vertical
y diagonal. Ninguna casilla lleva más de una
bomba, y donde hay número no hay bomba. Junto a
cada campo se da el total exacto de bombas que
contiene.
 |

|
|
|
|
| |
|
|
|
|
S O L U C I O N E S
|
1) |
 |
|
2) |
a) 16061
b) 55 km/h |
|
3) |
4 pájaros y
3 jaulas. |
|
4) |
a) Debatir
en clase
b)
 2 2
c) Por
ejemplo 21x (22+33)
d) Divido
por 4 y luego por 2
|
|
5) |
Hay que
retroceder 5 páginas. Las fechas son 10, 11,
12, y 13 de marzo. |
|
6) |
3 CD’s y 5
libros. |
|
7) |
Irlanda. |
|
8) |
En el año
2021. |
|
9) |
 |
|
10) |
a) 876543;
b) 65536, c) 420; d) 350; e) 2705; f) 12500. |
|
11) |
a) 19
b) 1
c) 4
d) 1
e) 8
f) 28 |
|
12) |
Debatir en
clase. |
|
13) |
a) 10
c) 2 y 5
b) 12
d) 17 |
|
14) |
3.773.519 GISELLE |
|
15) |
15
galletas. |
|
16) |
A = 12,75
cm; L = 25,5 cm. |
|
17) |
a) 3m y 0,5625 m2
b) 2,5 m y 0,25 m2
c) 3,5 m y 0,75 m2
d) 4m y 0,8125 m2
e) 4m y 0,4375 m2 |
|
18) |
150° |
|
19) |
 
|
|
20) |
Los
factores son 287 y 23, y el producto 6601 |
|
21) |

|
|
22) |

|
|
23) |

|
|
24) |
 |
|
25) |
 |
|
26) |

|
|
1)
La cantidad de fósforos que empleó Lolo para
escribir su nombre le alcanza para dibujar
cuatro cuadrados aunque, al dibujarlos,
pueden verse cinco en realidad. ¿Cómo lo
hace? |
 |
|
2)
¿Cómo pueden ubicarse tres fósforos sobre
una mesa sin que las cabezas de los tres
toquen dicha mesa? |
3)
Una persona quiere vender su caballo y el comprador
le pide precio. El dueño del caballo dice: “El
caballo tiene cuatro herraduras y cada herradura
tiene seis clavos. Me vas a pagar una moneda por el
primer clavo, dos por el segundo, cuatro por el
tercero, ocho por el cuarto y así hasta los 24
clavos de las herraduras del caballo”
¿Cuántas monedas vale este caballo?
4)
¿QUIÉN ES CULPABLE? Cuatro muchachos de 6to año son
sospechosos de haber escondido las meriendas de sus
compañeros. Estas son sus respuestas a las preguntas
del profesor encargado de la investigación.
Antonio: - He visto a Carlos y a Luis entrar en la
clase antes de que toque el timbre, así que uno de
ellos debe ser el culpable.
Bernardo: - No he sido yo.
Carlos: -Ha sido Luis, lo he visto con un objeto
extraño en la mano.
Luis:
- Ha sido Bernardo, lo juro. Lo vi mientras huía.
Si
sólo uno de ellos miente, ¿quién es el culpable?
5)
Una persona ingresa en una bodega para comprar 4
litros de vino. El bodeguero, a quien se le han roto
todos los recipientes de un litro que suele emplear
como unidades de medida, se ve obligado a manejarse
de otra manera. A su disposición tiene:
a) Un recipiente A lleno de vino, con 8 litros de
capacidad.
b) Un recipiente B vacío, de 5 litros de capacidad.
c) Un recipiente C vacío, de 3 litros de capacidad.
¿Cómo
se arreglará el bodeguero para dar al cliente 4 de
los 8 litros de vino contenidos en el recipiente más
grande, usando como medida sólo los tres recipientes
A, B y C descriptos anteriormente?
|
6)
Jorge, Carla, Lorena, Mariano y Alan viven
en la misma manzana y son compañeros de
escuela.
a) Lorena y Mariano tienen cuatro familias
vecinas.
b) Carla tiene un compañero de escuela en
cada una de las dos viviendas vecinas.
c) Jorge es quien tiene más familias vecinas
en la manzana.
d) Lorena es vecina de Jorge y de Carla,
pero no de Alan.
e) Alan tiene cinco familias vecinas. |
 |
Si llamamos “vecinos” a quienes viven en casas con
terrenos linderos, y en cada terreno vive sólo una
familia en una única vivienda, ¿sabrías indicar
dónde vive cada niño?
7)
Dos alumnos, Alicia y Bernardo, tienen una
calculadora e ingresan el mismo número. Alicia
multiplica el número que ingresó por 3 y luego suma
4 al resultado obtenido. Bernardo multiplica el
número que ingresó por 2 y luego suma 7 al resultado
obtenido. Cuando terminan, se dan cuenta que sus
calculadoras muestran exactamente el mismo
resultado. ¿Qué número ingresaron al principio?
8)
Andrea, Beatriz, Carlos, Darío y Enrique, cinco
buenos amigos, se encuentran después de mucho tiempo
y deciden sacarse una foto para celebrar su
reencuentro. Entonces, se ubican uno al lado de
otro, pero siguiendo un orden preestablecido.
¿Cuántas fotografías pueden tomarse con distintas
maneras de ubicarse los amigos?
9)
En una Terminal parte un tren del ramal “A” cada
hora; uno del ramal “B”, cada hora y media; y uno
del ramal “C” cada 48 minutos. A las 8 horas salió
un tren de cada ramal, ¿a qué hora volverán a
coincidir los tres trenes en el horario de partida?
10)
En un estacionamiento hay una cierta cantidad de
autos. Si el total de ruedas es 216, ¿cuántos autos
hay?
Algunos de estos autos tienen dos puertas y otros,
cuatro puertas. Siendo que la cantidad total de
puertas es 186, ¿cuántos autos hay de cuatro puertas
y cuántos de dos puertas?
11)
Un coche recorre 20 kilómetros a una velocidad de 40
km/h, y otros 20 kilómetros a 60 km/h. ¿En cuánto
tiempo cubrió los 40 kilómetros?
|
12)
SUDOKU CON LETRAS: Completar los casilleros
vacíos con las letras A, B, C, D, E y F, de
modo que no se repita ninguna de ellas en
ninguna fila, columna ni en cada cuadrícula.
|
 |
13)
Números cruzados


|
14)
TAPICES MATEMÁTICOS:
Objetivo: Lograr el mayor puntaje final que
sea posible.
Ingresa con cero puntos por cualquiera de
las entradas en la parte superior del tapiz
y trata de acumular el mayor puntaje
posible, realizando las operaciones que se
indican en cada uno de los cuadros blancos,
hasta alcanzar algunas de las salidas en la
parte inferior.
Aclaración: El recorrido puede subir,
bajar, ir hacia los costados o
entrecruzarse. Se puede pasar dos veces por
un mismo número pero por distintos caminos,
no por el mismo. |
 |
|
15)En
el triángulo ABC el ángulo
 y y
 .
Si .
Si
 y y
 son
bisectrices, determine la amplitud del
ángulo son
bisectrices, determine la amplitud del
ángulo
 |

|
|
16)
KAKURO. Completar la cuadrícula con un
número en cada casilla del 1 al 9, sin
repetir ninguno en la misma fila o columna,
de manera que el total de la suma en cada
fila y columna resulte la cifra indicada.
|
 |
| |
|
|
17)
TANGRAM DE LLOYD:

Utilizando las cinco piezas del tangram de Lloyd y
sin superponerlas, armar las siguientes figuras:
a)
Un trapecio
isósceles. d) Un
triángulo rectángulo.
 
|
18)
Completar el siguiente cuadrado mágico de
modo tal que cada columna, fila o diagonal
sumen 15 . .
|
 |
19)
Un jarrón de la dinastía Ming, comprado hoy en $
3.000, aumenta su valor linealmente con el tiempo,
de modo tal que, después de 15 años valdrá $ 3.450.
Por otro lado, un
Buda de jade, comprado hoy en $4.000, valdrá dentro
de 20 años $4.400.¿ En que momento el valor de las
piezas será en mismo?
20)
Rómulo, el jardinero, recibió instrucciones para
construir un cantero: debe tener forma rectangular
con 16 metros de perímetro y la superficie debe ser
máxima para permitir trasplantar la mayor cantidad
de plantines.
¿Qué medidas debe
tener el cantero?
21)
Mi auto produce
diferentes ruidos y cada uno es consecuencia de una
sola acción. Cuando prendo el motor, abro la puerta
y apago las luces, se oye un plom y un bang. Cuando
abro la puerta, bajo la ventana y prendo la radio,
se oye un crok y un shhh. Cuando apago las luces,
abro la maletera y prendo la radio, se oye un crok y
un plom. Entonces, cuando abro la puerta, prendo el
motor y abro la maletera, se oye:
a) un crok.; b) un
bang;. c) un plom y un bang; d) un crok y un shhh.
|
22)
Hallar el área de un rectángulo sabiendo que
su diagonal vale 5 cm y que su
perímetro vale 14 cm.
|
 |
|
23)
Dado el siguiente cuerpo, escribe el
polinomio que represente su volumen en
función de la medida indicada como x. Si el
cuadrado de la base tiene un perímetro de 24
cm, determine el volumen del cuerpo.
|
 |
|
24)
Dado el siguiente cuerpo, escribe el
polinomio que represente su área total en
función de la medida indicada como x. Si la
base del paralelepípedo tiene un área de 200
cm2, ¿cuál será el área total?
|
 |
|
25)
Tomando como unidad de superficie el
cuadrado blanco, calcula el área del
triángulo.
|
 |
|
26)
¿Qué palabra se forma al superponer estos
rectángulos? |
 |
|
27)
Determine el perímetro de un triángulo
equilátero sabiendo que su altura mide 18
cm.
|
 |
|
28)
En esta suma cada letra representa una cifra
menor que cinco. Escribe el valor de cada
una de ellas.
|
 |
29)
CLASIFICACIONES: Deduzca los resultados de los seis
encuentros del cuadrangular de fútbol cuya tabla de
posiciones aparece a continuación. Recuerde: G,
partidos ganados; E, partidos empatados; P,
partidos perdidos; F, goles a favor y C,
goles en contra. Cada partido da 3 puntos al
ganador, 0 puntos al derrotado y 1 punto a cada uno
si es empate. Ayúdese con el pequeño esquema de la
derecha para anotar las soluciones.

S O L U C I O N E S
|
1) |
 |
|
2) |
 |
|
3) |
16.777.575 |
|
4) |
El
culpable es Luis. |
|
5) |
1ra
posible solución:
A =
3 B = 5 C = 0
A = 3 B = 2 C = 3
A = 6 B = 2 C = 0
A = 6 B = 0 C = 2
A = 1 B = 5 C = 2
A = 1 B = 4 C = 3
2da
posible solución:
A =
5 B = 0 C = 3
A =
5 B = 3 C = 0
A =
2 B = 3 C = 3
A =
2 B = 5 C = 1
A =
7 B = 0 C = 1
A =
7 B = 1 C = 0
A
= 4 B = 1 C = 3
|
|
6) |

|
|
7) |
Ingresaron el número 3. |
|
8) |
5! =
120 maneras distintas. |
|
9) |
A las
20 horas. |
|
10) |
Hay 54
autos en el estacionamiento: 15 son de
dos puertas y 39 son de cuatro puertas. |
|
11) |
En 50
minutos. |
|
12) |
 |
|
13) |

|
|
14) |
Debatir
en clase. |
|
15) |
131º |
|
16) |

|
|
17) |

 |
|
18) |

|
|
19) |
Después
de 100 años. |
|
20) |
Será un
cuadrado de 4 m de lado. |
|
21) |
Opción
b: un bang. |
|
22) |
12 cm2 |
|
23) |
V( 3 cm
) = 360 cm3 |
|
24) |
A( 5 cm
) = 1360 cm2 |
|
25) |
5
cuadraditos |
|
26) |

|
|
27) |
Aproximadamente 62,35 cm |
|
28) |

|
|
29) |

|
|


![]()
